10900. Хотите стать 2ⁿ - эром?

Игрок имеет вначале игры 1$, ему задают n вопросов. На каждом шаге игрок может остановиться и забрать деньги или ответить на вопрос. Если на вопрос дан неправильный ответ, то игра заканчивается и игрок уходит без денег. Иначе призовая сумма удваивается и игра продолжается. После получения ответа на n - ый вопрос игра заканчивается, и игрок получает всю выигранную сумму.

Известно, что вероятность правильного ответа на каждый вопрос равна p и равномерно распределена на отрезке [t .. 1].

Вход. Каждая строка содержит два числа: целое n (1 £ n £ 30) и действительное t (0 £ t £ 1). Последний тест содержит n = t = 0 и не обрабатывается.

Выход. Для каждого теста вывести величину ожидаемого выигрыша, если игрок будет придерживаться оптимальной стратегии. Результат округлять до трех десятичных знаков.

Пример входа

1 0.5
1 0.3
2 0.6
24 0.25
0 0

Пример выхода

1.500
1.357
2.560
230.138

РЕШЕНИЕ

вероятность

Анализ алгоритма

Пусть f(n, a) – максимально возможное значение выигрыша, если игроку будет задано n вопросов, а начальная сумма равна a. Если n = 0, то игрок остается с начальной суммой, то есть f(0, a) = a. Вероятность правильного ответа равна p, t £ p £ 1. Если на первый вопрос игрок отвечает правильно, то дальше ему остается ответить на n – 1 вопросов имея призовую сумму 2a. С вероятностью 1 – p дается неверный ответ, и деньги пропадают. То есть ожидаемая сумма выигрыша после первого ответа станет равной p * f(n – 1, 2a) + (1 – p) * 0 = p * f(n – 1, 2a). Если это значение больше предыдущей суммы a, то стоит отвечать на вопрос, иначе следует остановить игру. Ожидаемый выигрыш после ответа на вопрос составит max(a, p * f(n – 1, 2a)). Поскольку вероятность p равномерно распределена на отрезке [t .. 1], то

f(n, a) =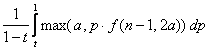

Если t = 1, то вероятность дать правильный ответ равна 1 и в таком случае следует отвечать на все n вопросов, получив при этом выигрыш 2ⁿ.

Пример

Рассмотрим третий тест, n = 2, t = 0.6. Начальный капитал a = 1.

f(2, 1) = , f(1, 2) = , f(0, 4) = 4

Вычислим значение f(1, 2) через f(0, 4):

f(1, 2) = = =

/ учитываем, что 4p > 2 при 0.6 £ p £ 1 /

= =

5 * (1 – 0.36) = 5 * 0.64 = 3.2

Вычислим значение f(2, 1) через f(1, 2):

f(2, 1) = = =

/ учитываем, что 3.2p > 1 при 0.6 £ p £ 1 /

= =

4 * (1 – 0.36) = 4 * 0.64 = 2.56

Реализация алгоритма

Функция integral вычисляет значение интеграла I(a, k) = для заданных действительных чисел a и k. При t = 1 вероятность угадывания p равна единице, значение интеграла I(a, k) полагается равным max(a, k).

Ниже приведена область, площадь которой равна значению интеграла :

Найдем точку пересечения прямых y = a и y = kp: a = kp, откуда p = a/k. Положим temp = a / k. Значение интеграла рассмотрим как сумму + . В зависимости от положения точки temp относительно точек t и 1 вычисляем значение интеграла I(a, k).

Если t £ temp £ 1, то + = a * (temp – t) + k * (1 – temp * temp) / 2.

Если temp £ t, то + = = k * (1 – t * t) / 2.

Если temp > 1, то + = = a * (1 – t).

double integral(double a, double k)

{

double s = 0, temp = a / k;

if (t == 1) return max(a,k);

if (temp > 1) return a * (1 - t);

if (temp >= t) s = a * (temp - t);

else temp = t;

s += k * (1 – temp * temp) / 2;

return s / (1 - t);

}

Рекурсивное вычисление f(n, a) = .

double f(int n, int a)

{

if (!n) return a;

double k = f(n-1,2*a);

return integral(a,k);

}

Основной цикл программы. Читаем входные данные и выводим значение f(n, 1).

while(scanf("%d %lf",&n,&t),n + t)

printf("%.3lf\n",f(n,1));